Introduction: Searching and sorting are fundamental operations in computer science and play a crucial role in various applications. In this blog post, we will delve into different searching and sorting algorithms, exploring their intricacies and implementations in Python. From linear search to quick sort, we will cover a range of algorithms and provide code examples for better understanding.
Searching Algorithms:
Searching is the process of finding a specific element (or multiple elements) within a collection of data. The collection can be an array, a list, a database, or any other data structure. The goal of searching is to locate the desired item(s) efficiently.
Linear Search

Linear search is a simple search algorithm that checks every element in the list sequentially until the desired element is found. It's easy to understand but not very efficient for large datasets.
Binary Search

Binary search is more efficient than linear search but requires the list to be sorted. It works by repeatedly dividing the search interval in half, significantly reducing the search space.
Sorting Algorithms:
Sorting is the process of arranging elements in a specified order, often ascending or descending based on some criteria. Sorting is essential for organizing data in a meaningful way, making it easier to search, analyze, and process.
Bubble Sort
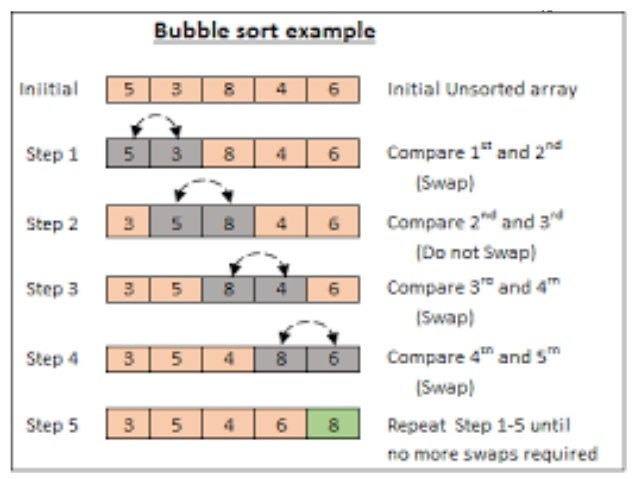
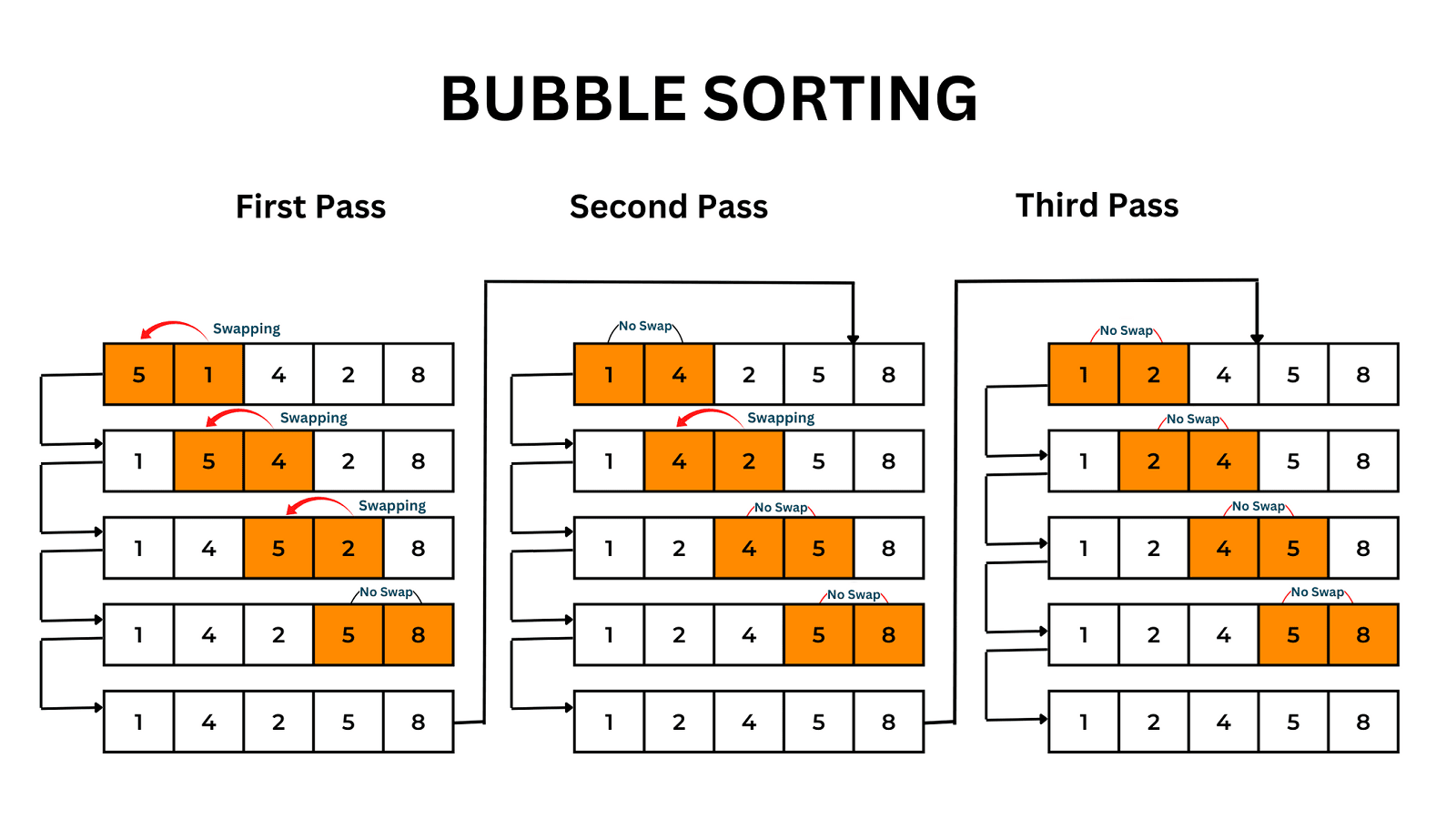
Bubble sort is a basic sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. While simple, it's inefficient for large lists.
Selection Sort

Selection sort finds the minimum element from the unsorted part and puts it at the beginning. It continues this process for the remaining elements, gradually building up the sorted array.
Insertion Sort

Insertion sort builds a sorted array by repeatedly taking the next element from the unsorted part and inserting it into its correct position in the sorted part. It's efficient for small datasets and nearly sorted lists.
Merge Sort

Merge sort divides the unsorted list into sublists, each containing one element, and repeatedly merges sublists to produce new sorted sublists. It's a recursive algorithm with better performance than bubble and selection sort for larger datasets.
Quick Sort

Quick sort picks an element as a pivot and partitions the array around the pivot, ensuring that elements smaller than the pivot are on the left and elements larger are on the right. It recursively applies this process to the sub-arrays, leading to efficient sorting.
Python Code Examples:
Now, let's dive into the Python code examples for each algorithm, demonstrating their application to an example list [64, 34, 25, 12, 22, 11, 90]. These code snippets will showcase how to implement these algorithms and their results.
1. Linear Search:
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
# Example list
example_list = [64, 34, 25, 12, 22, 11, 90]
target = 22
print("Linear Search:", linear_search(example_list, target))
2. Binary Search:
def binary_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
# Example list must be sorted for binary search
example_list.sort()
target = 22
print("Binary Search:", binary_search(example_list, target))
3. Bubble Sort:
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
# Create a copy of the example list for sorting
bubble_sorted_list = example_list.copy()
bubble_sort(bubble_sorted_list)
print("Bubble Sort:", bubble_sorted_list)
4. Selection Sort:
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
# Create a copy of the example list for sorting
selection_sorted_list = example_list.copy()
selection_sort(selection_sorted_list)
print("Selection Sort:", selection_sorted_list)
5. Insertion Sort:
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# Create a copy of the example list for sorting
insertion_sorted_list = example_list.copy()
insertion_sort(insertion_sorted_list)
print("Insertion Sort:", insertion_sorted_list)
6. Merge Sort:
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
L = arr[:mid]
R = arr[mid:]
merge_sort(L)
merge_sort(R)
i = j = k = 0
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < len(L):
arr[k] = L[i]
i += 1
k += 1
while j < len(R):
arr[k] = R[j]
j += 1
k += 1
# Create a copy of the example list for sorting
merge_sorted_list = example_list.copy()
merge_sort(merge_sorted_list)
print("Merge Sort:", merge_sorted_list)
7. Quick Sort:
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
# Create a copy of the example list for sorting
quick_sorted_list = example_list.copy()
quick_sorted_list = quick_sort(quick_sorted_list)
print("Quick Sort:", quick_sorted_list)
By mastering these searching and sorting algorithms, you'll enhance your problem-solving skills and gain valuable insights into algorithmic efficiency and performance optimization.
Conclusion:
In this blog post, we've explored various searching and sorting algorithms in Python, ranging from linear search to quick sort. Each algorithm has its unique characteristics and applications, and understanding them is essential for any programmer. With the provided code examples and explanations, you're now equipped to apply these algorithms to solve real-world problems effectively. Happy coding!
